Negotiation 101: What is the pie?

This week I was browsing through some Coursera courses and I bumped into an interesting course about negotiation. This is a course offered to the business school students. I never really liked business courses. But this title seemed interesting. So, I thought of giving it a try. After all, we negotiate all the time. I did not expect this course to be math heavy. However, the instructor presented some intriguing math in the first module. I thought of sharing it with you.

In this post we will only explore a simplified negotiation scenario. Two party negotiations where both parties know everything. Such simplification is often a good idea to learn more complex scenarios later on. Let’s take a particular example. We have our beloved cartoon characters Tom and Jerry as negotiators. Jerry is a skilled mouse. He can make a cake of size 1 unit on his own. On the other hand, Tom is more skilled than Jerry. He can make a cake of size 2 units on his own. But, if they combine their forces and make a cake together, they can make a cake of size 9 units. Obviously, it makes sense for them to make the cake together. However, the problem is, how to divide the size 9 cake after they make it?

A simple solution is to divide the cake equally. 4.5 units each. This is the starting point. Obviously, it is clear that Jerry gets more benefit from this deal than Tom. So, Tom will not agree to it. He is more skilled, after all.

Another solution is to divide the cake in proportion to their skills. Tom is twice as skilled as Jerry. Therefore, Tom would get ⅔ of the cake that is 6 units. Jerry will get the remaining 3 units. This seems quite fair.

But Jerry is smart. He thinks he can get more. His argument is based on a fundamental question for negotiation.

What is the pie?

Yes, we are talking about cake, but the pie in the question is about what are we negotiating about? The pie that they are trying to divide is the added benefit of combining their forces. Jerry can make a cake of size 1 unit on his own. Tom can make a cake of size 2 units on his own. The added benefit they get for making the cake together is hence 9 - (1 + 2) = 6 units. This is the extra benefit that they are negotiating over. This is the pie.

In other words, Tom will never accept a division in which he gets less than size 2. That much he can make it himself. So, Tom can just take the 2 units of the cake without even asking Jerry. Similarly, Jerry can take 1 unit of the cake without even asking Tom. The leftover is 6 units. This is what they are trying to divide.

While it might seem that the remaining 6 units should be divided in proportion to their skills, it is not a fair division. Participation from both is equally required to gain that extra benefit of 6 units. If any one of them decides to not participate, the benefit just goes away. Since both parties have equal power, it makes sense to divide the pie equally. That is, 3 units for Tom and 3 units for Jerry. In total, Jerry gets 4 units (1 he took earlier and 3 from the pie) and Tom gets 5 units. This is the fairest division both parties can get.

Let’s take a more complex example. This time, Tom and Jerry go out for dinner. The restaurant serves a bottle of wine. Here is the table describing how much Tom or Jerry would be willing to pay for the wine.

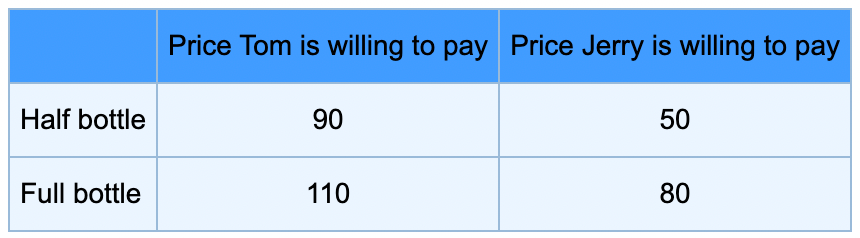
The restaurant only serves full bottles and one bottle costs 100$. The question is whether they should share a bottle or not? If they share a bottle, how much Tom should pay for it? Clearly, Tom values the wine more. So, he should pay more. But how much exactly? Is a 70-30 cost split fair?

Before learning about the concept of pie, I would not be able to figure out the fair price for Tom. But the pie concept makes it simple. What is the pie here? If they share the cost and buy a bottle, they both get half the bottle, that is $40 ($90 + $50 - $100) worth of benefit. Tom on his own can buy a bottle and get $10 worth of benefit. Jerry can’t do the same. So on their own, they can get the benefit of 10$. So the pie is 40 - 10 = $30.

The splitting part is simple. Since both of them are required to participate to get the added benefit, the pie is split evenly ($15 each). For Jerry, it means paying $35 ($50 - half the pie) and for Tom, the amount is 65$ ($90 - $10 - half the pie).

This simple tool makes negotiation simpler. Of course, the real-world scenarios are often more complex. The simplifying assumption we made might not be valid. It can involve more than two parties. Not each party would know about the cost/benefits of the other parties. But, the simplified scenario covers a large portion of the real-world negotiations we do. Knowing the “fair” value gives us an advantage while negotiating. This simplified scenario can also form the base for learning the more complex scenarios.

My Favorites:

Video of the week: Popular bad life advises

Quote of the week: “The opposite of love is indifference, and the opposite of happiness is boredom.” ― Timothy Ferriss, The 4-Hour Workweek